Jedna věc, kterou budeme dělat hodně s algoritmy v této sérii je graf traversal. Co to přesně znamená?
v podstatě je myšlenka, že se budeme pohybovat kolem grafu z jednoho vrcholu do druhého a objevovat vlastnosti jejich vzájemně propojených vztahů.
dva z nejčastěji používaných algoritmů, které budeme hodně používat, jsou: Depth-First Search (DFS) a width-First Search (BFS).,
zatímco oba tyto algoritmy nám umožňují procházet grafy, liší se různými způsoby. Začněme s DFS.
DFS využívá ve své implementaci filozofii „go deep, head first“. Myšlenka je, že počínaje počátečním vrcholem (nebo místem) jdeme po jedné cestě, dokud nedosáhneme konce, a pokud nedosáhneme cíle, vrátíme se a půjdeme jinou cestou.
podívejme se na příklad., Předpokládejme, že máme orientovaný graf, který vypadá takhle:

Teď je v plánu, že začneme na vrchol s a jsme žádal, aby našel vrchol t. Pomocí DFS, jdeme prozkoumat jednu cestu, jít celou cestu až do konce a pokud nenajdeme t, pak jsme se jít dolů jinou cestu., Tady je postup:

Tak tady jsme šli cestou (p1) první sousední vrchol a vidíme, že to není konec, protože to má cesta k další vrchol., Tak jsme se jít po této cestě:
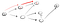
Toto je zjevně není vrchol t, takže se musíme vrátit, protože jsme ve slepé uličce. Vzhledem k tomu, že předchozí uzel již nemá sousedy, vracíme se do s., Z s, jsme se jít do jeho druhé sousední uzel:
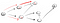
Jít po cestě (p2), jsme konfrontováni se třemi sousedy., Od první, kdo již navštívil, musíme jít po druhý:
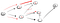
Nyní, opět jsme se dostali do slepé uličky, že to není vrchol t, takže se musíme vrátit., Protože tam je další soused, který nebyl navštívil, jsme se jít dolů, že sousední cesty a konečně jsme našli vrcholu t:

to je To, jak DFS funguje. Jděte po cestě a pokračujte, dokud nedosáhnete cíle nebo slepé uličky. Pokud je to cíl, máte hotovo. Pokud tomu tak není, pak se vraťte a pokračujte jinou cestou, dokud nevyčerpáte všechny možnosti v této cestě.,
můžeme vidět, že jsme stejný postup na každý vrchol, který jsme navštívili:
DFS pro každý soused vrcholu
Protože to znamená dělat stejný postup na každý krok, něco nám říká, že budeme muset použít rekurzi k provedení tohoto algoritmu.
Zde je kód v Javascriptu:
Poznámka: Tento specifický DFS algoritmus nám umožňuje zjistit, zda je možné se dostat z jednoho místa na druhé., DFS lze použít různými způsoby a mohou existovat jemné změny algoritmu výše. Obecný koncept však zůstává stejný.
analýza DFS
nyní analyzujeme tento algoritmus. Vzhledem k tomu, že procházíme každým sousedem uzlu a ignorujeme navštívené, máme runtime O(V + E).
rychlé vysvětlení, co přesně V+E znamená:
V. představuje celkový počet vrcholů. E představuje celkový počet hran. Každý vrchol má řadu hran.,
i když se může zdát, že člověk může být veden k přesvědčení, že je v * e místo V + E, pojďme přemýšlet o tom, co v•e přesně znamená.aby něco bylo V * E, znamenalo by to, že pro každý vrchol se musíme podívat na všechny hrany v grafu bez ohledu na to, zda jsou tyto hrany spojeny s tímto konkrétním vrcholem.
zatímco na druhé straně V + E znamená, že pro každý vrchol se díváme pouze na počet okrajů, které se týkají tohoto vrcholu. Připomeňme si z předchozího příspěvku, že prostor, který zabíráme pro seznam adjacency, je O (v + E)., Každý vrchol má řadu hran a v nejhorším případě, kdybychom měli spustit DFS na každém vrcholu, udělali bychom O (V) práci spolu s prozkoumáním všech okrajů vrcholů, což je O(E). Jakmile jsme se podívali na všechny V počet vrcholů, bychom se také podíval na celkem e hrany. Proto je V + e.
nyní, protože DFS používá rekurzi na každém vrcholu, to znamená, že se používá zásobník (proto se nazývá chyba přetečení zásobníku, kdykoli narazíte na nekonečné rekurzivní volání). Proto je prostorová složitost O (V).,
nyní se podívejme, jak se liší první vyhledávání.
šířka-první vyhledávání
šířka-první vyhledávání (BFS) následuje filozofii „go wide, bird ‚ s eye-view“. To v podstatě znamená, že místo toho, aby šel celou cestu dolů po jedné cestě až do konce, BFS se pohybuje směrem k cíli jednoho souseda najednou., Pojďme se podívat na to, co to znamená:

Takže místo toho jen jít celou cestu dolů jeho první soused, BFS by navštívit všechny sousedy s první, a pak navštivte ty sousedy, se sousedy a tak dále, dokud se nedosáhne t.,fd17d“> 

See how different DFS and BFS behave?, I když si rád myslím, že DFS rád jde hlavou, BFS rád vypadá pomalu a pozoruje vše jeden krok po druhém.
nyní by měla být jedna otázka, která nám vyčnívá: „jak víme, které sousedy nejprve navštívit od sousedů s?“
No, mohli bychom využít fronta je first-in-first-out (FIFO) majetek, kde jsme se pop první vrchol z fronty, přidejte jeho nenavštívené sousedy do fronty, a pak pokračujte v tomto procesu do fronty, je buď prázdná, nebo vrchol přidáme do něj je vrchol jsme hledali.,
Nyní se pojďme podívat na kód v Javascriptu:
Analýza BFS
To se může zdát jako BFS je pomalejší. Ale pokud se podíváte pozorně na vizualizace obou BFS a DFS, zjistíte, že ve skutečnosti mají stejný runtime.
fronta zajišťuje, že maximálně každý vrchol bude zpracován,dokud nedosáhne cíle. To znamená, že v nejhorším případě se BFS také podívá na všechny vrcholy a všechny hrany.,
Zatímco BFS může zdát pomalejší, je to vlastně považují za rychlejší, protože pokud bychom měli realizovat na větší grafy, zjistíte, že DFS odpady hodně času jít dolů dlouhé cesty, které jsou nakonec špatně. Ve skutečnosti se BFs často používá v algoritmech k určení nejkratší cesty z jednoho vrcholu do druhého, ale na ty se dotkneme později.
Tak od runtimes jsou stejné, BFS má runtime o(V + E) a vzhledem k použití fronty, který může držet na většině V. vrcholy, má paměťovou složitost O(V).,
analogie k odchodu s
chci vás nechat pryč jinými způsoby, které si osobně Představuji, jak DFS a BFS pracují v naději, že vám také pomůže zapamatovat si.
kdykoli přemýšlím o DFS, rád přemýšlím o něčem, co najde správnou cestu tím, že narazí do mnoha slepých uliček. Obvykle by to bylo jako myši procházející bludištěm, aby hledaly jídlo.,bych zkusit cestu, zjistili, že cesta je slepá ulička, pak pivot na další cestu a opakujte tento proces, dokud nedosáhne svého cíle:

A to je to, co zjednodušenou verzi procesu by vypadat takto:

pro BFS, Vždycky jsem si to představoval jako vlnění.,div>

stejně jako, jak BFS začíná u zdroje a návštěvy zdroj sousedů první a pak jde více směrem ven tím, že navštívíte své sousedy, a tak dále:

Shrnutí
- prohledávání do Hloubky (DFS) a prohledávání do Šířky (BFS) jsou oba slouží k procházení grafů.,
- DFS se nabíjí po jedné cestě, dokud nevyčerpá tuto cestu k nalezení svého cíle, zatímco BFS se vlní přes sousední vrcholy, aby našel svůj cíl.
- DFS používá zásobník, zatímco BFS používá frontu.
- oba DFS a BFS mají runtime O (v + E) a prostorovou složitost O(V).
- oba algoritmy mají různé filozofie, ale sdílejí stejný význam v tom, jak procházíme grafy.