Rozdělení pravděpodobnosti | Typy Rozdělení

Úvod

Vítejte do světa Pravděpodobnosti v Data Science! Dovolte mi začít věci s intuitivním příkladem.

Předpokládejme, že jste učitel na univerzitě. Po kontrole úkolů po dobu jednoho týdne jste klasifikovali všechny studenty. Dal jste tyto odstupňované papíry na zadávání dat chlapa na univerzitě a řekněte mu, aby vytvořit tabulku obsahující známky všech studentů., Ale ten chlap ukládá pouze známky a ne odpovídající studenty.

udělal další chybu, ve spěchu zmeškal několik záznamů a nemáme tušení, jejichž známky chybí. Pojďme najít způsob, jak to vyřešit.

jedním ze způsobů je vizualizace stupňů a zjistit, zda v datech najdete trend.

graf, který máte, se nazývá frekvenční distribuce dat. Vidíte, že existuje hladká křivka jako struktura, která definuje naše data, ale všimnete si anomálie?, Máme abnormálně nízkou frekvenci v určitém rozsahu skóre. Takže nejlepší odhad by bylo mít chybějící hodnoty, které odstraní zub v distribuci.

takto byste se pokusili vyřešit problém v reálném životě pomocí analýzy dat. Pro každého datového vědce, studenta nebo praktika je distribuce nutností znát koncept. Poskytuje základ pro analytické a inferenční statistiky.

zatímco pojem pravděpodobnosti nám dává matematické výpočty, distribuce nám pomáhají skutečně vizualizovat, co se děje pod ním.,

v tomto článku jsem se zabýval některými důležitými rozděleními pravděpodobnosti, které jsou vysvětleny přehledným i komplexním způsobem.

Poznámka: Tento článek předpokládá, že máte základní znalosti o pravděpodobnosti. Pokud tomu tak není, můžete odkazovat na rozdělení pravděpodobnosti.,

Obsah

Společné Datové Typy
Druhy Rozdělení
1. Bernoulliho Distribuce
2. Rovnoměrné Rozložení
3. Binomické Rozdělení
4. Normální Rozdělení
5. Poissonovo Rozdělení
6. Exponenciální Rozdělení.
Vztahy mezi Distribucí
Otestujte své Znalosti!

běžné datové typy

než přejdeme k vysvětlení distribucí, uvidíme, s jakými daty se můžeme setkat. Data mohou být diskrétní nebo spojitá.,

diskrétní Data, jak název napovídá, mohou mít pouze zadané hodnoty. Například, když hodíte kostkou, možné výsledky jsou 1, 2, 3, 4, 5 nebo 6 a ne 1.5 nebo 2.45.

kontinuální Data mohou mít libovolnou hodnotu v daném rozsahu. Rozsah může být konečný nebo nekonečný. Například hmotnost nebo výška dívky, délka silnice. Hmotnost dívky může být libovolná hodnota od 54 kg nebo 54,5 kg nebo 54,5436 kg.

nyní začněme s typy distribucí.,

typy distribucí

Bernoulli distribuce

začněme s nejjednodušší distribucí, která je Bernoulli distribuce. Je to vlastně snazší pochopit, než to zní!

všichni kriket feťáci tam venku! Na začátku každého kriketového zápasu, jak se rozhodnete, kdo bude netopýr nebo míč? Hod! Vše záleží na tom, zda vyhrajete nebo prohrajete Los, že? Řekněme, že pokud hod povede k hlavě, vyhrajete. Jinak prohraješ. Není žádná střední cesta.

distribuce Bernoulli má pouze dva možné výsledky, a to 1 (úspěch) a 0 (selhání) a jeden pokus., Takže náhodná proměnná X, která má Bernoulliho distribuce může mít hodnotu 1 s pravděpodobností úspěchu, říkají, p a hodnoty 0 s pravděpodobností selhání, řekněme q nebo 1-p.

Tady, výskyt hlavu označuje úspěch, a výskyt ocas označuje selhání.
pravděpodobnost získání hlavy = 0,5 = pravděpodobnost získání ocasu, protože existují pouze dva možné výsledky.

hmotnostní funkce pravděpodobnosti je dána: px(1-p) 1-x, kde x € (0, 1).,
To můžeme také zapsat jako

pravděpodobnosti úspěchu a neúspěchu nemusí být stejně pravděpodobné, jako výsledek boje mezi mnou a Undertaker. Je si jistý, že vyhraje. Takže v tomto případě je pravděpodobnost mého úspěchu 0,15, zatímco moje selhání je 0,85

zde, pravděpodobnost úspěchu (p) není stejná jako pravděpodobnost selhání. Takže níže uvedený graf ukazuje rozložení Bernoulliho našeho boje.

zde je pravděpodobnost úspěchu = 0,15 a pravděpodobnost selhání = 0,85., Očekávaná hodnota je přesně to, co to zní. Když tě praštím, možná budu čekat, že mě praštíš zpátky. V podstatě očekávaná hodnota jakékoli distribuce je průměr distribuce., Očekávaná hodnota náhodné proměnné X z Bernoulliho rozdělení je nalezena takto:

E(X) = 1*p + 0*(1-p) = p,

rozptyl náhodné proměnné z bernoulliho rozdělení je:

V(X) = E(X2) – 2 = p – p2 = p(1-p)

Existuje mnoho příkladů z Bernoulliho rozdělení, jako je, zda to bude zítra pršet, nebo ne, kde se déšť označuje úspěch a žádný déšť označuje selhání a Vítězství (úspěch) nebo ztráty (poruchy) hru.

rovnoměrné rozložení

když hodíte spravedlivou matrici, výsledky jsou 1 až 6., Pravděpodobnosti získání těchto výsledků jsou stejně pravděpodobné a to je základ jednotného rozdělení. Na rozdíl od Bernoulliho rozdělení jsou všechny n počet možných výsledků rovnoměrného rozdělení stejně pravděpodobné.

proměnná X je řekl, aby byl rovnoměrně distribuován, jestliže hustota pravděpodobnosti je:

graf rovnoměrné rozložení křivka vypadá jako …

můžete vidět, že tvar Rovnoměrné rozložení křivky je obdélníkový, důvod, proč Rovnoměrné rozdělení se nazývá obdélníkové rozdělení.,

pro rovnoměrné rozdělení jsou parametry a A b.

počet kytic prodávaných denně v květinářství je rovnoměrně rozložen s maximálně 40 a minimálně 10.

zkusme vypočítat pravděpodobnost, že denní prodej klesne mezi 15 a 30.

pravděpodobnost, že denní tržby se pohybují mezi 15 a 30 je (30-15)*(1/(40-10)) = 0.5

Podobně, pravděpodobnost, že denní tržby jsou větší než 20 je = 0.,667

průměr a rozptyl X následující rovnoměrné rozdělení je:

– > E(X) = (a+b)/2

Rozptyl -> V(X) = (b-a)2/12

standardní jednotnou hustotu má parametry a = 0 a b = 1, tak PDF pro standardní uniformu hustota je dána tím, že:

Binomické Rozdělení

vraťme se k kriket. Předpokládejme, že jste dnes vyhráli hod a to znamená úspěšnou událost. Zase házíš, ale tentokrát jsi prohrál., Pokud dnes vyhrajete hod, nevyžaduje to, že zítra vyhrajete hod. Přiřaďte náhodnou proměnnou, řekněme X, kolikrát jste vyhráli hod. Jaká může být možná hodnota X? Může to být libovolné číslo v závislosti na tom, kolikrát jste hodili minci.

existují pouze dva možné výsledky. Hlava označující úspěch a ocas označující selhání. Proto pravděpodobnost získání hlavy = 0,5 a pravděpodobnost selhání lze snadno vypočítat jako: q = 1-p = 0,5.,

distribuce, kde jsou možné pouze dva výsledky, jako je úspěch nebo selhání, zisk nebo ztráta, výhra nebo prohra a kde je pravděpodobnost úspěchu a selhání stejná pro všechny zkoušky, se nazývá Binomická distribuce.

výsledky nemusí být stejně pravděpodobné. Vzpomínáte si na příklad boje mezi mnou a Undertakerem? Pokud je tedy pravděpodobnost úspěchu v experimentu 0,2, pravděpodobnost selhání lze snadno vypočítat jako q = 1-0,2 = 0,8.

každá zkouška je nezávislá, protože výsledek předchozího hodu neurčuje ani neovlivňuje výsledek aktuálního hodu., Experiment s pouze dvěma možnými výsledky opakovaných n počet krát se nazývá binomický. Parametry binomické distribuce jsou n A p, kde n je celkový počet pokusů a p je pravděpodobnost úspěchu v každém pokusu.

na základě výše uvedeného vysvětlení jsou vlastnosti binomické distribuce

každá studie je nezávislá.
ve zkoušce jsou pouze dva možné výsledky – buď úspěch, nebo selhání.
provádí se celkový počet n identických studií.
pravděpodobnost úspěchu a neúspěchu je stejná pro všechny zkoušky., (Zkoušky jsou totožné.,

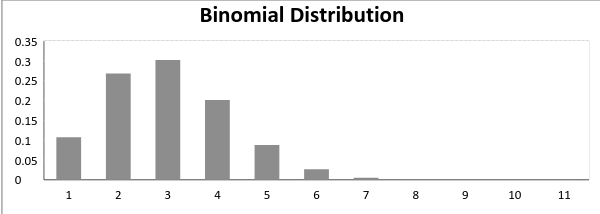
Nyní, když pravděpodobnost úspěchu = pravděpodobnost selhání, v takové situaci graf binomického rozdělení vypadá to,

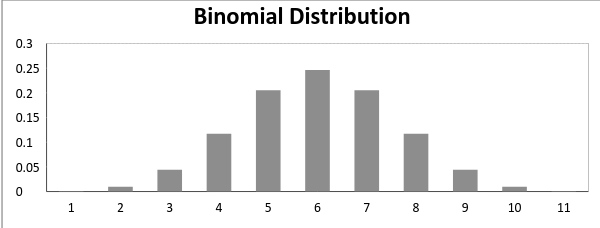
průměr a rozptyl binomického rozdělení jsou dány:

– > µ = n*p

Rozptyl -> Var(X) = n*p*q

Normální Rozdělení

Normální rozdělení představuje chování většiny situací ve vesmíru (To je důvod, proč je nazývá „normální“ distribuce., Hádám!). Velký součet (malých) náhodných proměnných se často ukazuje jako normálně distribuovaný, což přispívá k jeho rozšířené aplikaci. Jakákoli distribuce je známá jako normální distribuce, pokud má následující vlastnosti:
1. střední, střední a způsob distribuce se shodují.
2. křivka distribuce je zvonovitá a symetrická kolem čáry x = μ.
3. celková plocha pod křivkou je 1.
4. přesně polovina hodnot je vlevo od středu a druhá polovina vpravo.,
normální distribuce se velmi liší od binomické distribuce. Pokud se však počet pokusů přiblíží nekonečnu, budou tvary docela podobné.

PDF náhodné veličiny X na základě normálního rozdělení je dána tím, že:

průměr a rozptyl náhodné veličiny X, který je řekl, aby byl normální rozdělení je dána tím, že:

– > E(X) = µ

Rozptyl -> Var(X) = σ^2

Tady, µ (střední hodnota) a σ (směrodatná odchylka) jsou parametry.,
graf náhodné proměnné X ~ N (µ, σ) je uveden níže.

standardní normální distribuce je definována jako distribuce se střední hodnotou 0 a směrodatnou odchylkou 1. Pro takový případ, PDF stane:

Poissonovo Rozdělení

Předpokládejme, že budete pracovat v call centru, přibližně, kolik hovorů se dostanete za den? Může to být libovolné číslo. Nyní je celý počet hovorů v call centru za den modelován poissonovou distribucí., Některé další příklady jsou
1. počet tísňových volání zaznamenaných v nemocnici za den.
2. počet krádeží hlášených v oblasti za den.
3. počet zákazníků, kteří přijedou do salonu za hodinu.
4. počet sebevražd hlášených v konkrétním městě.
5. počet tiskových chyb na každé stránce knihy.
nyní si můžete představit mnoho příkladů po stejném kurzu., Poissonova distribuce je použitelná v situacích, kdy se události vyskytují v náhodných časových bodech a prostoru, přičemž náš zájem spočívá pouze v počtu událostí události.

distribuce se nazývá Poissonova distribuce, pokud jsou platné následující předpoklady:

1. Každá úspěšná událost by neměla ovlivnit výsledek jiné úspěšné události.
2. Pravděpodobnost úspěchu v krátkém intervalu se musí rovnat pravděpodobnosti úspěchu v delším intervalu.
3. Pravděpodobnost úspěchu v intervalu se blíží nule, protože interval se zmenšuje.,

Nyní, pokud nějaká distribuce ověřuje výše uvedené předpoklady, pak je to Poissonova distribuce. Některé zkratky používané v Poissonovo rozdělení, jsou:
- λ je rychlost, při které dojde k události,
- t je délka časového intervalu,
- A X je počet událostí v časovém intervalu.
zde se X nazývá Poissonova náhodná proměnná a rozdělení pravděpodobnosti X se nazývá Poissonova distribuce.

nechť µ označuje průměrný počet událostí v intervalu délky t.pak µ = λ*t.,

PMF X po poissonově distribuci je dána:

průměrný µ je parametrem této distribuce. µ je také definována jako délka λ krát tohoto intervalu. Graf poissonovy distribuce je uveden níže:

níže uvedený graf znázorňuje posun křivky v důsledku zvýšení průměru.

je patrné, že jak se průměr zvyšuje, křivka se posune doprava.,

průměr a rozptyl X následující Poissonovo rozdělení:

– > E(X) = µ
Rozptyl -> Var(X) = µ

Exponenciální Rozdělení

podívejme se na call centru například jeden více času. A co časový interval mezi hovory ? Tady, exponenciální distribuce přichází k naší záchraně. Exponenciální distribuční modely interval času mezi hovory.

Další příklady jsou:

1. Doba příjezdu metra beteeen,
2., Doba mezi příjezdy na čerpací stanici
3. Životnost klimatizace

exponenciální distribuce je široce používána pro analýzu přežití. Od očekávané životnosti stroje až po očekávaný život člověka, exponenciální distribuce úspěšně přináší výsledek.

náhodné proměnné X je řekl, aby měl exponenciální rozdělení s PDF:

f(x) = { λe-λx, x ≥ 0,

a parametr λ>0, který je také nazýván rychlost.,

Pro analýzu přežití, λ se nazývá míra selhání zařízení v každém čase t, vzhledem k tomu, že to přežilo až do „t“.

průměr a Rozptyl náhodné proměnné X po exponenciální rozdělení:

– > E(X) = 1/λ,

Rozptyl -> Var(X) = (1/λ)2

Také, čím větší je frekvence, tím rychleji křivka klesá a nižší rychlost, plošší křivku. To je vysvětleno lépe s grafem uvedeným níže.,

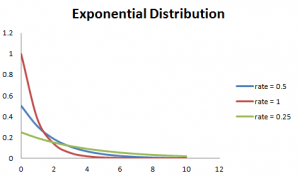
pro usnadnění výpočtu jsou uvedeny níže uvedené vzorce.
P{X≤x} = 1 – e-λx, odpovídá ploše pod hustotou křivka vlevo od x.

P{X>x} = e-λx, odpovídá ploše pod hustotou křivku do prava z x.

P{x1<X≤ x2} = e-λx1 – e-λx2, odpovídá ploše pod hustotou křivky mezi x1 a x2.

vztahy mezi distribucí

vztah mezi Bernoulli a binomickou distribucí

1., Bernoulli distribuce je zvláštní případ binomické distribuce s jediným soudem.

2. Existují pouze dva možné výsledky Bernoulli a binomické distribuce, a to úspěch a neúspěch.

3. Bernoulli i binomické distribuce mají nezávislé stezky.

Vztahu mezi Poissonovo a Binomické Rozdělení

Poissonovo Rozdělení je limitujícím případě binomické rozdělení za následujících podmínek:
1. počet pokusů je neomezeně velké nebo n → ∞.,
2. pravděpodobnost úspěchu pro každou zkoušku je stejná a neurčitě malá nebo p →0.
3. np = λ, je konečný.
Vztahu mezi Normální a Binomické Rozdělení & Normální a Poissonovo Rozdělení:

Normální rozdělení je dalším omezujícím formě binomické rozdělení za následujících podmínek:
1. počet pokusů je neomezeně velké, n → ∞.
2. p i q nejsou neomezeně malé.
normální distribuce je také omezujícím případem poissonovy distribuce s parametrem λ →∞.,

Vztahu mezi Exponenciální a Poissonovo Rozdělení:

v Případě, že časy mezi náhodné události postupujte podle exponenciálního rozdělení s rychlostí λ, potom celkový počet událostí v časovém období délky t sleduje Poissonovo rozdělení s parametrem λt.

Otestujte si své znalosti

došli jste tak daleko. Nyní jste schopni odpovědět na následující otázky? Dejte mi vědět v komentářích níže!

1. Vzorec pro výpočet standardní normální náhodné proměnné je:

a. (x+µ) / σ
b. (x-µ) / σ
c. (x-σ) / µ

2., V Bernoulliho Rozdělení, vzorce pro výpočet směrodatné odchylky je dána vztahem:

. p (1 – p)
b. SQRT(p(p – 1))
c. SQRT(p(1 – p))

3. Pro normální rozdělení, což představuje nárůst v průměru bude:

. posun křivky doleva.
b. posun křivky doprava
c. zploštit křivku

4. Životnost baterie je exponenciálně distribuována s λ = 0,05 za hodinu. Pravděpodobnost, že baterie vydrží mezi 10 a 15 hodinami, je:

a. 0.1341
b.0.1540
c. 0.,0079

Poznámky

Rozdělení Pravděpodobnosti jsou převládající v mnoha odvětvích, a sice, pojištění, fyzika, strojírenství, počítačová věda, a dokonce i sociální vědy, kde studenti psychologie a lékařské jsou široce pomocí rozdělení pravděpodobnosti. Má snadnou aplikaci a široké použití. Tento článek zdůraznil šest důležitých distribucí, které jsou pozorovány v každodenním životě a vysvětlily jejich aplikaci. Nyní budete moci identifikovat, vztahovat a rozlišovat mezi těmito distribucemi.,

Pokud máte nějaké pochybnosti a chcete vidět další články o distribucích, napište prosím do sekce komentářů níže. Pro podrobnější zápis těchto distribucí můžete tento zdroj odkázat.