One thing that we’ll be doing a lot with the algorithms in this series is graph traversal. O que significa isto exactamente?
basicamente, a idéia é que nós vamos nos mover em torno do grafo de um vértice para outro e descobrir as propriedades de suas relações interconectadas.
dois dos algoritmos mais comumente usados que vamos usar um lote é: Profundidade-primeira pesquisa (DFS) e largura-primeira pesquisa (BFS).,
embora ambos os algoritmos nos permitam atravessar grafos, eles diferem de várias maneiras. Vamos começar pelo DFS.
DFS utiliza a filosofia “go deep, head first” em sua implementação. A idéia é que a partir de um vértice inicial (ou lugar), vamos por um caminho até chegarmos ao fim e se não chegarmos ao nosso destino, então voltamos e seguimos um caminho diferente.vejamos um exemplo., Suponha que nós temos um gráfico direcionado parecido com este:

Agora, a idéia é a de que temos que começar pelo vértice s e somos solicitados a encontrar o vértice t. Usando o DFS, vamos explorar um caminho, vá todo o caminho até o fim e, se não encontrar t, então vamos por outro caminho., Aqui está o processo:

Então, aqui, nós vamos para baixo o caminho (p1) do primeiro vizinhos do vértice e vemos que ele não é o fim, porque ele tem um caminho em direção a outro vértice., Então, temos que ir por esse caminho:
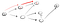
Evidentemente, este não é o vértice de t, então nós temos que voltar, porque chegamos a um beco sem saída. Como o nó anterior não tem mais vizinhos, voltamos ao S., A partir de s, podemos ir para o segundo nó vizinho:
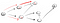
a descer o caminho (p2), estamos confrontados com três vizinhos., Desde que o primeiro já tenha sido visitado, temos que ir até o segundo:
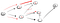
Agora, mais uma vez chegamos a um beco sem saída, que não é o vértice de t então, nós temos que voltar., Uma vez que não há outro vizinho que ainda não foi visitado, o que os vizinhos caminho e finalmente encontramos o vértice de t:

Esta é a forma como DFS obras. Segue por um caminho e continua até chegares ao destino ou a um beco sem saída. Se é o destino, acabou. Se não for, então volte e continue por um caminho diferente até que você tenha esgotado todas as opções dentro desse caminho.,
podemos ver que seguimos o mesmo procedimento em cada vértice que nós, visite:
um DFS para cada vizinho do vértice
uma vez que este implica em fazer o mesmo procedimento em cada passo, algo nos diz que vamos precisar usar recursão para implementar esse algoritmo.
Aqui está o código em JavaScript:
Nota: Este DFS específico algoritmo permite-nos determinar se é possível chegar de um lugar para outro., DFS pode ser usado em uma variedade de maneiras e pode haver mudanças sutis no algoritmo acima. No entanto, o conceito geral permanece o mesmo.
Análise de DFS
Agora vamos analisar este algoritmo. Uma vez que estamos atravessando cada vizinho do nó e estamos ignorando os visitados, temos um tempo de execução de O(V + E).
a quick explanation of exactly what V+e means:
v represents the total number of vertices. E representa o número total de arestas. Cada vértice tem um número de arestas., embora possa parecer que alguém pode ser levado a acreditar que é V•e em vez de V + E, vamos pensar sobre o que v•e significa exatamente.
para algo ser V•e, isso significaria que para cada vértice, temos que olhar para todas as arestas no grafo, independentemente se essas arestas estão ou não conectadas a esse vértice específico.
While, on the other hand, V + e means that for each vertex, we only look at the number of edges that pertain to that vertex. Lembre-se do post anterior, que o espaço que ocupamos para a lista de adjacência é O(V + E)., Cada vértice tem um número de arestas e, no pior dos casos, se fizéssemos DFS em cada vértice, nós teríamos feito O(V) trabalhar junto com a exploração de todas as arestas dos vértices, que é O(E). Uma vez que tenhamos olhado para todo o número V de vértices, nós também teríamos olhado para um total de arestas E. Portanto, é V + E.
Agora, pois DFS usa recursão em cada vértice, o que significa que uma pilha é usada (que é por que ele é chamado de erro de estouro de pilha sempre que você executar em um infinito chamada recursiva). Portanto, a complexidade do espaço é O(V).,
Agora vamos ver como largura-primeira pesquisa difere.
largura-primeira pesquisa
largura-primeira pesquisa (BFS) segue a filosofia “ir largo, visão de pássaro”. O que isso basicamente significa é que em vez de percorrer todo o caminho até o fim, a BFS se move em direção ao seu destino um vizinho de cada vez., Vejamos o que isso significa:

Assim, em vez de apenas ir toda a maneira para baixo sua primeira vizinho, BFS iria visitar todos os vizinhos de s primeiro e, em seguida, visitar os vizinhos e os vizinhos e assim por diante, até atingir t.,fd17d”> 

See how different DFS and BFS behave?, Enquanto eu gosto de pensar que o DFS gosta de ir de frente, o BFS gosta de olhar devagar e observar tudo um passo de cada vez.
agora uma questão que se destaca para nós deve ser: “como sabemos quais vizinhos visitar primeiro dos vizinhos de s?”
Bem, poderíamos utilizar uma fila de first-in-first-out (FIFO) propriedade onde nós pop o primeiro vértice da fila, adicionar a sua unvisited vizinhos de fila e, em seguida, continue esse processo até que a fila esteja vazia ou o vértice adicionamos isso é o vértice estamos procurando.,
Agora vamos ver o código em JavaScript:
a Análise de BFS
pode parecer BFS é mais lento. Mas se você olhar cuidadosamente para as visualizações de ambos BFS e DFS, você vai descobrir que eles realmente têm o mesmo tempo de execução.
a fila garante que, no máximo, cada vértice será processado até chegar ao destino. Isso significa que no pior caso, BFS também olhará para todos os vértices e todas as arestas.,
embora BFS possa parecer mais lento, na verdade é considerado mais rápido porque se nós os implementássemos em grafos maiores, você descobrirá que DFS desperdiça muito tempo descendo por longos caminhos que, em última análise, estão errados. Na verdade, BFS é muitas vezes usado em algoritmos para determinar o caminho mais curto de um vértice para outro, mas vamos tocar neles mais tarde.
assim, uma vez que os tempos de execução são os mesmos, BFS tem um tempo de execução de O(V + e) e devido ao uso de uma fila que pode manter no máximo V vértices, ele tem uma complexidade de espaço de O(V).,
analogias para deixar de fora com
i want to leave you off with other ways that I personally imagine how DFS and BFS work in hopes that it will help you remember as well.
sempre que penso em DFS, gosto de pensar em algo que encontra o caminho certo ao esbarrar em muitos becos sem saída. Normalmente, isto seria como um rato a atravessar um labirinto para procurar comida.,gostaria de tentar um caminho, descobrir que o caminho é um beco sem saída, em seguida, rode-o para outro caminho e repita esse processo até que ele atinja o seu alvo:

E este é uma versão simplificada do processo de como seria:

Agora, para BFS, Eu sempre imaginei ele como uma onda.,div>

assim como o BFS começa na fonte e visitas a origem de seus vizinhos em primeiro lugar e, em seguida, vai mais para o exterior, visitando seus vizinhos e assim por diante:

Resumo
- Depth-First Search (DFS) e Amplitude-First Search (BFS) são utilizados tanto para atravessar gráficos.,
- DFS carrega por um caminho até que tenha esgotado esse caminho para encontrar o seu alvo, enquanto BFS ondula através de vértices vizinhos para encontrar o seu alvo.
- DFS usa uma pilha enquanto BFS usa uma fila.ambos DFS e BFS têm um tempo de execução de O (V + E) e uma complexidade de espaço de O(V).ambos os algoritmos têm filosofias diferentes, mas partilham igual importância na forma como atravessamos grafos.