Distribuição de probabilidade / tipos de distribuições

introdução

Bem-vindo ao mundo da probabilidade na ciência dos dados! Permitam-me que comece com um exemplo intuitivo.suponha que é professor numa universidade. Depois de verificar as tarefas durante uma semana, classificou todos os alunos. Deste estes papéis graduados a um tipo da universidade e diz-lhe para criar uma folha de cálculo com as notas de todos os alunos., Mas o tipo só guarda as notas e não os alunos correspondentes.

ele fez outro erro, ele perdeu um par de entradas em uma pressa e não temos idéia de quais as notas estão faltando. Vamos encontrar uma maneira de resolver isto.

uma maneira é que você visualize as notas e veja se você pode encontrar uma tendência nos dados.

o gráfico que você tem é chamado de distribuição de frequência dos dados. Você vê que há uma curva suave como a estrutura que define os nossos dados, mas você percebe uma anomalia?, Temos uma frequência anormalmente baixa num determinado intervalo de pontuação. Então o melhor palpite seria ter valores em falta que removem a amolgadela na distribuição.

é assim que você tentaria resolver um problema da vida real usando a análise de dados. Para qualquer cientista de dados, estudante ou praticante, a distribuição é um conceito que deve saber. Ele fornece a base para a análise e estatística inferencial.

enquanto o conceito de probabilidade nos dá os cálculos matemáticos, as distribuições ajudam-nos a visualizar o que está a acontecer por baixo.,

neste artigo, eu cobri algumas distribuições de probabilidade importantes que são explicadas de forma lúcida, bem como abrangente.Nota: Este artigo assume que você tem um conhecimento básico de probabilidade. Se não, você pode se referir a estas distribuições de probabilidade.,

Índice

Tipos de Dados Comuns
Tipos de Distribuições
1. Distribuição de Bernoulli
2. Distribuição Uniforme
3. Distribuição Binomial
4. Distribuição Normal
5. Distribuição de Poisson
6. Distribuição Exponencial
Relações entre as Distribuições
Teste o seu Conhecimento!

tipos de dados comuns

Antes de saltarmos para a explicação das distribuições, vamos ver que tipo de dados podemos encontrar. Os dados podem ser discretos ou contínuos.,

dados discretos, como o nome sugere, podem tomar apenas valores especificados. Por exemplo, quando você rola um dado, os resultados possíveis são 1, 2, 3, 4, 5 ou 6 e não 1.5 ou 2.45.os dados contínuos podem ter qualquer valor dentro de uma dada gama. A gama pode ser finita ou infinita. Por exemplo, o peso ou a altura de uma menina, O comprimento da estrada. O peso de uma menina pode ser qualquer valor de 54 kgs, ou 54,5 kgs, ou 54,5436 kgs.

agora vamos começar com os tipos de distribuições.,

tipos de distribuições

distribuição de Bernoulli

vamos começar com a distribuição mais fácil que é a distribuição de Bernoulli. É realmente mais fácil de entender do que parece!todos vocês viciados em críquete! No início de qualquer jogo de críquete, como você decide quem vai bater ou jogar? Um lançamento! Tudo depende de ganhares ou perderes o lançamento, certo? Digamos que se o lançamento resultar em uma cabeça, você ganha. Senão, perdes. Não há midway.

uma distribuição de Bernoulli tem apenas dois resultados possíveis, nomeadamente 1 (sucesso) e 0 (fracasso), e um único ensaio., Assim, a variável aleatória X tem uma distribuição de Bernoulli pode tomar o valor 1 com probabilidade de sucesso, digamos p, e o valor 0 com probabilidade de falha, dizer q ou 1-p.

Aqui, a ocorrência de uma cabeça denota sucesso, e a ocorrência de uma cauda indica falha.probabilidade de ter uma cabeça = 0,5 = probabilidade de ter uma cauda, uma vez que há apenas dois resultados possíveis.

a função de massa de probabilidade é dada por: px(1-p)1-x em que x € (0, 1).,
também pode ser escrito como

As probabilidades de sucesso e fracasso não precisa ser igualmente prováveis, como o resultado de uma luta entre mim e Undertaker. Ele tem quase a certeza que vai ganhar. Assim, neste caso a probabilidade de meu sucesso é 0,15 enquanto minha falha é 0,85

Aqui, a probabilidade de sucesso(p) não é a mesma que a probabilidade de fracasso. Então, o gráfico abaixo mostra a distribuição Bernoulli da nossa luta.

Aqui, a probabilidade de sucesso = 0.15 e a probabilidade de fracasso = 0.85., O valor esperado é exatamente o que parece. Se te esmurrar, espero que me retribuas. Basicamente o valor esperado de qualquer distribuição é a média da distribuição., O valor esperado de uma variável aleatória X a partir de uma distribuição de Bernoulli é encontrada da seguinte forma:

E(X) = 1*p + 0*(1-p) = p

A variância de uma variável aleatória a partir de uma distribuição de bernoulli é:

V(X) = E(X2) – 2 = p – p2 = p(1-p)

Existem muitos exemplos de distribuição de Bernoulli, tais como as para saber se vai chover amanhã, ou não, de onde a chuva indica sucesso e sem chuva denota fracasso e Vitória (sucesso) ou perder (falha) o jogo.

distribuição uniforme

quando se rola um dado justo, os resultados são de 1 a 6., As probabilidades de obter estes resultados são igualmente prováveis e essa é a base de uma distribuição uniforme. Ao contrário da distribuição de Bernoulli, todos os n Número de resultados possíveis de uma distribuição uniforme são igualmente prováveis.

Uma variável X é dito ser uniformemente distribuída, se a função de densidade é:

O gráfico de uma distribuição uniforme curva parece

Você pode ver que a forma da distribuição Uniforme curva é retangular, a razão pela qual a distribuição Uniforme é chamado retangular de distribuição.,para uma distribuição uniforme, A E b são os parâmetros.

O número de ramos vendidos diariamente numa florista é uniformemente distribuído com um máximo de 40 e um mínimo de 10.vamos tentar calcular a probabilidade de as vendas diárias descerem entre 15 e 30.

a probabilidade de as vendas diárias diminuírem entre 15 e 30 é (30-15)*(1/(40-10)) = 0.5

similarmente, a probabilidade de as vendas diárias serem superiores a 20 é = 0.,667

a média e A variância de X a seguir uma distribuição uniforme é:

Média> E(X) = (a+b)/2

de Variância> V(X) = (b-a)2/12

O padrão de densidade uniforme tem parâmetros a = 0 e b = 1, então o PDF para o padrão de densidade uniforme é dado por:

Distribuição Binomial

Vamos voltar para o críquete. Suponha que você ganhou o lançamento hoje e isso indica um evento bem sucedido. Voltas a atirar, mas desta vez perdeste., Se você ganhar um arremesso hoje, isso não precisa que você vai ganhar o arremesso amanhã. Vamos atribuir uma variável aleatória, digamos X, ao número de vezes que ganhou o lançamento. Qual pode ser o possível valor de X? Pode ser qualquer número dependendo do número de vezes que você jogou uma moeda.existem apenas dois resultados possíveis. Cabeça denotando sucesso e cauda denotando fracasso. Portanto, a probabilidade de obter uma cabeça = 0.5 e a probabilidade de falha pode ser facilmente computada como: q = 1 – p = 0.5.,

uma distribuição onde apenas dois resultados são possíveis, tais como sucesso ou fracasso, ganho ou perda, vitória ou perda e onde a probabilidade de sucesso e falha é a mesma para todos os ensaios é chamada de distribuição Binomial.não é necessário que os resultados sejam igualmente prováveis. Lembras-te do exemplo de uma luta entre mim e o Undertaker? Então, se a probabilidade de sucesso em um experimento é 0.2 então a probabilidade de falha pode ser facilmente computada como q = 1 – 0.2 = 0.8.

cada ensaio é independente uma vez que o resultado do lançamento anterior não determina ou afeta o resultado do lançamento atual., Um experimento com apenas dois resultados possíveis repetidos n Número de vezes é chamado binomial. Os parâmetros de uma distribuição binomial São N E p Onde n é o número total de ensaios e p é a probabilidade de sucesso em cada ensaio.

com base na explicação acima, as propriedades de uma distribuição Binomial são

cada ensaio é independente.há apenas dois resultados possíveis num ensaio-um sucesso ou um fracasso.
um número total de n ensaios idênticos são realizados.
a probabilidade de sucesso e fracasso é a mesma para todos os ensaios., (Os ensaios são idênticos.,

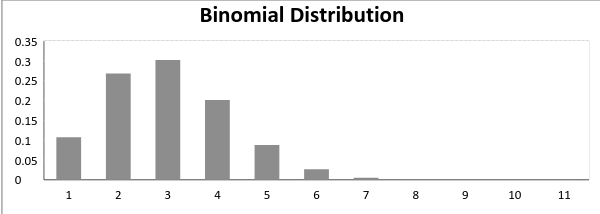
Agora, quando a probabilidade de sucesso = probabilidade de falha, em tal situação, o gráfico da distribuição binomial parece

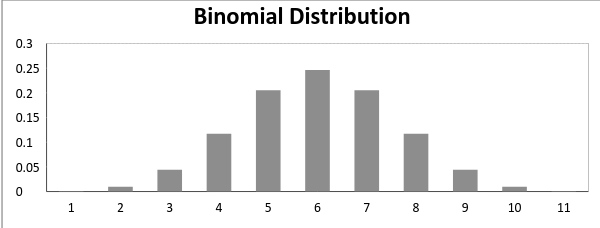
A média e variância de uma distribuição binomial são dadas por:

Média> µ = n*p

Desvio -> Var(X) = n*p*q

Distribuição Normal

distribuição Normal representa o comportamento da maioria das situações em que o universo (é por isso Que ele é chamado de “normal” de distribuição., Acho que sim!). A grande soma de (pequenas) variáveis aleatórias muitas vezes acaba por ser normalmente distribuída, contribuindo para a sua aplicação generalizada. Qualquer distribuição é conhecida como distribuição Normal se tiver as seguintes características:
1. A média, mediana e modo de distribuição coincidem.
2. a curva da distribuição é em forma de sino e simétrica em relação à linha x=μ.a área total sob a curva é 1.
3. exatamente metade dos valores estão à esquerda do centro e a outra metade à direita.,
uma distribuição normal é muito diferente da distribuição Binomial. No entanto, se o número de ensaios se aproximar do infinito, então as formas serão bastante semelhantes.

O PDF de uma variável aleatória X a seguir uma distribuição normal é dada por:

A média e variância de uma variável aleatória X, que é dito ser distribuídos normalmente é dado por:

Média> E(X) = µ

de Variância> Var(X) = σ^2

Aqui, µ (média) e σ (desvio padrão) são os parâmetros.,
O grafo de uma variável aleatória X ~ N (µ, σ) é mostrado abaixo.

Uma distribuição normal padrão é definida como a distribuição com média 0 e desvio padrão 1. Para tal caso, o PDF torna-se:

a Distribuição de Poisson

Suponha que você trabalha em um call center, aproximadamente, quantas chamadas você começa em um dia? Pode ser qualquer número. Agora, todo o número de chamadas num centro de chamadas num dia é modelado pela distribuição de Poisson., Alguns outros exemplos são
1. o número de chamadas de emergência gravadas em um hospital em um dia.
2. o número de roubos notificados numa área num dia.o número de clientes que chegam a um salão dentro de uma hora.o número de suicídios notificados numa determinada cidade.
3. o número de erros de impressão em cada página do livro.
Você pode agora pensar em muitos exemplos seguindo o mesmo curso., A distribuição de Poisson é aplicável em situações em que os eventos ocorrem em pontos aleatórios de tempo e espaço em que nosso interesse reside apenas no número de ocorrências do evento.

uma distribuição é chamada de distribuição de Poisson quando os seguintes pressupostos são válidos:

1. Qualquer evento bem sucedido não deve influenciar o resultado de outro evento bem sucedido.
2. A probabilidade de sucesso em um intervalo curto deve igualar a probabilidade de sucesso em um intervalo mais longo.
3. A probabilidade de sucesso em um intervalo se aproxima de zero à medida que o intervalo se torna menor.,

Agora, se qualquer distribuição valida os pressupostos acima, então é uma distribuição de Poisson. Algumas notações utilizadas na distribuição de Poisson são:
- λ é a taxa na qual um evento ocorre,
- t é o comprimento de um intervalo de tempo,
- E X é o número de eventos em um intervalo de tempo.
Aqui, X é chamado de uma variável aleatória de Poisson e a distribuição de probabilidade de X é chamada de distribuição de Poisson.

let µ denote the mean number of events in an interval of length T. Then, µ = λ * T.,

O PMF de X a seguir uma distribuição de Poisson é dada por:

A média µ é o parâmetro de distribuição. µ é também definido como o comprimento λ vezes desse intervalo. O gráfico de uma distribuição de Poisson é mostrado abaixo:

o gráfico mostrado abaixo ilustra o deslocamento na curva devido ao aumento da média.

é perceptível que, à medida que a média aumenta, a curva muda para a direita.,

a média e A variância de X a seguir uma distribuição de Poisson:

Média> E(X) = µ
de Variância> Var(X) = µ

Distribuição Exponencial

Vamos considerar o call center exemplo mais uma vez. E o intervalo de tempo entre as chamadas ? Aqui, a distribuição exponencial vem em nosso auxílio. A distribuição exponencial modela o intervalo de tempo entre as chamadas.outros exemplos são:

1. Comprimento do tempo de chegada do metro beteeen,
2., Período de tempo entre as chegadas a um posto de gasolina
3. A vida útil de um ar condicionado

distribuição exponencial é amplamente utilizada para a análise da sobrevivência. Da vida esperada de uma máquina à vida esperada de uma distribuição exponencial humana resulta com sucesso o resultado.

Uma variável aleatória X é dita ter uma distribuição exponencial com o PDF:

f(x) = { λe-λx, x ≥ 0

e o parâmetro λ>0, o que também é chamado de taxa.,

Para a análise de sobrevida, λ é chamado a taxa de falha de um dispositivo, em qualquer tempo t, dado que sobreviveu até t.

Média e Variância de uma variável aleatória X seguindo uma distribuição exponencial:

Média> E(X) = 1/λ

Desvio -> Var(X) = (1/λ)2

além disso, quanto maior a taxa, mais rapidamente a curva cai e menor a taxa, mais plana da curva. Isto é explicado melhor com o gráfico mostrado abaixo.,

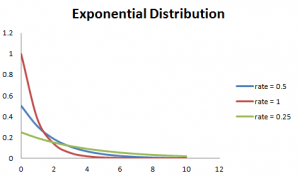
para facilitar o cálculo, existem algumas fórmulas dadas abaixo.
P{X≤x} = 1 – e-λx, corresponde à área sob a curva de densidade para a esquerda de x.

P{X>x} = e-λx, corresponde à área sob a curva de densidade para a direita de x.

P{x1<X≤ x2} = e-λx1 – e-λx2, corresponde à área sob a curva de densidade entre x1 e x2.

relações entre as distribuições

relação entre Bernoulli e distribuição Binomial

1., A distribuição de Bernoulli é um caso especial de distribuição Binomial com um único julgamento.2. Há apenas dois resultados possíveis de uma distribuição Bernoulli e Binomial, ou seja, sucesso e fracasso.3. Ambas as distribuições de Bernoulli e Binomial têm trilhas independentes.

A relação entre Poisson e distribuição Binomial

distribuição Poisson é um caso limitante de distribuição binomial nas seguintes condições:
1. o número de ensaios é indefinidamente grande ou n → ∞.,
2. a probabilidade de sucesso para cada ensaio é a mesma e indefinidamente pequena ou p →0.
3. np = λ, é finito.
Relação entre o Normal e Distribuição Binomial & Normal e Distribuição de Poisson:

distribuição Normal é outra limitação forma de distribuição binomial sob as seguintes condições:
1. O número de tentativas é indefinidamente grande, n → ∞.ambos p E q não são indefinidamente pequenos.
a distribuição normal é também um caso limitante de distribuição de Poisson com o parâmetro λ →∞.,

Relação entre a Exponencial e a Distribuição de Poisson:

Se os tempos entre eventos aleatórios siga distribuição exponencial com taxa λ, então o número total de eventos em um período de tempo de duração t segue a distribuição de Poisson com parâmetro λt.teste o seu conhecimento. Agora, você é capaz de responder às seguintes perguntas? Deixe-me saber nos comentários abaixo!1. A fórmula para calcular a variável aleatória normal padrão é:

um. (x+µ) / σ
b. (x-µ) / σ
c. (x-σ) / µ

2., Na Distribuição de Bernoulli, a fórmula para calcular o desvio padrão é dado por:

um. p (1 – p)
b. SQRT(p(p – 1))
c. SQRT(p(1 – p))

3. Para uma distribuição normal, um aumento da média será:

um. deslocar a curva para a esquerda
b. deslocar a curva para a direita
c. achatar a curva

4. A vida útil de uma bateria é exponencialmente distribuída com λ = 0,05 por hora. A probabilidade de uma bateria para durar entre 10 e 15 horas é:

um.0.1341
b.0.1540
c.0.,0079

End Notes

Probability Distributions are prevalent in many sectors, namely, insurance, physics, engineering, computer science and even social science wherein the students of psychology and medical are widely using probability distributions. Tem uma aplicação fácil e uso generalizado. Este artigo destacou seis distribuições importantes que são observadas no dia-a-dia e explicou sua aplicação. Agora você será capaz de identificar, relacionar e diferenciar entre essas distribuições.,

Se tiver dúvidas e quiser ver mais artigos sobre distribuições, por favor escreva na secção de comentários abaixo. Para uma escrita mais aprofundada destas distribuições, você pode consultar este recurso.